Acrobot Simulation Robustness Leaderboard

Controller	Short Controller Description	Model [%]	Velocity Noise [%]	Torque Noise [%]	Torque Step Response [%]	Time delay [%]	Overall Robustness Score	Username	Data
iLQR MPC stabilization	Online optimization with iterative LQR. Stabilization of iLQR trajectory. Top stabilization with LQR.	13.8	90.5	100.0	90.5	47.6	0.685	fwiebe	Data and Plots
TVLQR	Stabilization of iLQR trajectory with time-varying LQR.	59.0	95.2	100.0	100.0	76.2	0.861	fwiebe	Data and Plots
SAC LQR	Swing-up with an RL Policy learned with SAC.	76.7	71.4	100.0	100.0	61.9	0.820	chiniklas	Data and Plots
iLQR Riccati Gains	Stabilization of iLQR trajectorry with Riccati gains. Top stabilizaion with LQR.	6.2	28.6	38.1	71.4	4.8	0.298	fwiebe	Data and Plots
mcpilco	Swingup trained with MBRL algorithm MC-PILCO + stabilization with LQR.	40.5	66.7	81.0	90.5	19.0	0.595	turcato-niccolo	Data and Plots
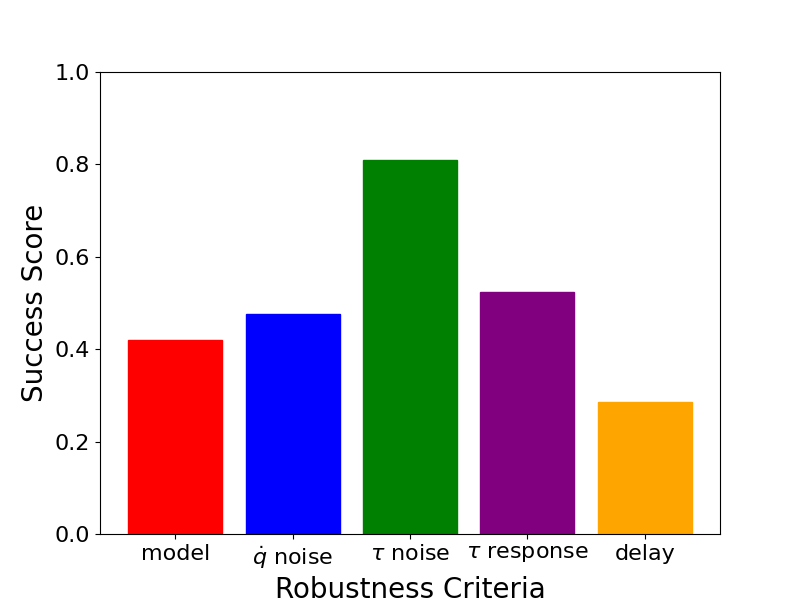
Energy PFL	Partial Feedback Linearization with energy shaping control. Stabilization with LQR.	41.9	47.6	81.0	52.4	28.6	0.503	fwiebe	Data and Plots
iLQR MPC	Online optimization with iterative LQR. Without reference trajectory.	20.5	4.8	4.8	9.5	4.8	0.089	fwiebe	Data and Plots

Rules

The robustness leaderboard compares the performance of different control methods by perturbing the simulation e.g. with noise or delay. The task for the controller is to swingup and balance the acrobot even with these perturbations.

The model parameters of the acrobot are:

Gravity: $g = 9.81 \, \frac{\text{m}}{\text{s}^2}$
First Link mass: $m_1 = 0.6416937799349799 \, \text{kg}$
Second Link mass: $m_2 = 0.563935954099688 \, \text{kg}$
First actuator length: $l_1 = 0.2 \, \text{m}$
Second actuator length: $l_2 = 0.3 \, \text{m}$
First link center of mass: $r_1 = 0.2 \, \text{m}$
Second link center of mass: $r_2: 0.3212669909674605 \, \text{m}$
First link inertia: $I_1 = 0.02671076499939512 \, \text{kg m}^2$
Second link inertia: $I_2 = 0.053878129629650884 \, \text{kg m}^2$
First actuator damping friction: $b_1 = 0.0 \, \frac{\text{kg m}}{s}$
Second actuator damping friction: $b_2 = 0.0 \, \frac{\text{kg m}}{s}$
First actuator coulomb friction: $c_{f1}: 0.0 \, \text{N m}$
Second actuator coulomb friction: $c_{f2}: 0.0 \, \text{N m}$
Motor Inertia: $I_r = 0.0 \, \text{kg m}^2$
Gear ratio: $g_r: 6.0$
First Motor Torque limit $\tau_{max1} = 0.0 \, \text{N m}$
Second Motor Torque limit $\tau_{max2} = 6.0 \, \text{N m}$

More information about the dynamic model of the double pendulum can be found here: Double Pendulum Dynamics. For a urdf file with this model see here: URDF.

The acrobot is simulated with a Runge-Kutta 4 integrator with a timestep of $dt = 0.002 \, \text{s}$ for $T = 10 \, \text{s}$. The initial acrobot configuration is $x_0 = (0.0, 0.0, 0.0, 0.0)$ (hanging down) and the goal is the unstable fixpoint at the upright configuration $x_g = (\pi, 0.0, 0.0, 0.0)$. The upright position is considered to be reached when the distance in the state coordinates is below $\epsilon = (0.1, 0.1, 0.5, 0.5)$.

Scores

For the evaluation multiple criteria are evaluated and weighted to calculate an overall score (Real AI Score). The criteria are:

Model inaccuracies $c_{model}$: The model parameters, that have been determined with system identification, will never be perfectly accurate. To asses inaccuracies in these parameters, we vary the independent model parameters one at the time in the simulator while using the original model parameters in the controller.
Measurement noise $c_{vel, noise}$: The controllers’ outputs depend on the measured system state. In the case of the QDDs, the online velocity measurements are noisy. Hence, it is important for the transferability that a controller can handle at least this amount of noise in the measured data. The controllers are tested with and without a low-pass noise filter.
Torque noise c_{, noise}$: Not only the measurements are noisy, but also the torque that the controller outputs is not always exactly the desired value.
Torque response $c_{\tau, response}$: The requested torque of the controller will in general not be constant but change during the execution. The motor, however, is sometimes not able to react immediately to large torque changes and will instead overshoot or undershoot the desired value. This behavior is modelled by applying the torque $\tau = \tau_{t-1} + k_{resp} (\tau_{des} - \tau_{t-1})$ instead of the desired torque $\tau_{des}$. Here, $\tau_{t-1}$ is the applied motor torque from the last time step and $k_{resp}$ is the factor which scales the responsiveness. $k_{resp} = 1$ means the torque response is perfect while $k_{resp} \neq 1$ means the motor is over/undershooting the desired torque.
Time delay $c_{delay}$: When operating on a real system there will always be time delays due to communication and reaction times.

For each crierion the quantities are varied in $N=21$ steps (for the model inaccuracies for each independent model parameter) and the score is the percentage of successful swingups.

These criteria are used to calculate the overall Real AI Score with the formula

\[ S = w_{model} c_{model} + w_{vel, noise} c_{vel, noise} + w_{\tau, noise} c_{\tau, noise} + w_{\tau, response} c_{\tau, response} + w_{delay} c_{delay} \]

The weights are

\[ w_{model} = w_{vel, noise} = w_{\tau, noise} = w_{\tau, response} = w_{delay} = 0.2 \]

Participating

If you want to participate in this leaderboard with your own controller have a look at the leaderboard explanation in the double pendulum repository. The leaderboard is automatically periodically updated based on the controllers that have been contributed to that repository.